the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The effect of a loss of model structural detail due to network skeletonization on contamination warning system design: case studies
Michael J. Davis
Robert Janke
The effect of limitations in the structural detail available in a network model on contamination warning system (CWS) design was examined in case studies using the original and skeletonized network models for two water distribution systems (WDSs). The skeletonized models were used as proxies for incomplete network models. CWS designs were developed by optimizing sensor placements for worst-case and mean-case contamination events. Designs developed using the skeletonized network models were transplanted into the original network model for evaluation. CWS performance was defined as the number of people who ingest more than some quantity of a contaminant in tap water before the CWS detects the presence of contamination. Lack of structural detail in a network model can result in CWS designs that (1) provide considerably less protection against worst-case contamination events than that obtained when a more complete network model is available and (2) yield substantial underestimates of the consequences associated with a contamination event. Nevertheless, CWSs developed using skeletonized network models can provide useful reductions in consequences for contaminants whose effects are not localized near the injection location. Mean-case designs can yield worst-case performances similar to those for worst-case designs when there is uncertainty in the network model. Improvements in network models for WDSs have the potential to yield significant improvements in CWS designs as well as more realistic evaluations of those designs. Although such improvements would be expected to yield improved CWS performance, the expected improvements in CWS performance have not been quantified previously. The results presented here should be useful to those responsible for the design or implementation of CWSs, particularly managers and engineers in water utilities, and encourage the development of improved network models.
- Article
(762 KB) -
Supplement
(1119 KB) - BibTeX
- EndNote
Author Michael J. Davis's copyright for this publication is transferred to UChicago Argonne, LLC as operator of Argonne National Laboratory: the submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a US Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The US government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the government. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan, last access: 23 April 2018).
Water distribution systems (WDSs) can be contaminated intentionally by the injection of a contaminant into the system or accidentally, for example, by releases of contaminants into reservoirs or by contaminated water entering the distribution system when adequate pressure is not maintained. Sensors designed to detect potential contaminants can provide a warning that a system has been contaminated and reduce potential consequences associated with a contamination event. The design of contamination warning systems (CWSs) employing multiple sensors has been an active research area; Hart and Murray (2010) have reviewed strategies for placement of sensors in CWSs. Given that a CWS may be able to help reduce consequences associated with contamination events, understanding the factors that can affect the quality of a CWS design is important for those responsible for managing distribution systems. This paper focuses on one important factor, the accuracy with which the network model of a distribution system represents the actual structural details of the network, namely its pipes and junctions.
Lack of structural detail in the network models developed for WDSs is known to reduce the accuracy of estimated adverse health effects associated with potential contamination events in these systems (Bahadur et al., 2008; Davis and Janke, 2014; Grayman and Rhee, 2000; Grayman et al., 1991; Janke et al., 2007, 2009). Lack of network model detail is also known to affect sensor placement in the design of CWSs (Klise et al., 2013). All network models involve some degree of simplification relative to the actual WDS. Although improvements in network models would be expected to result in improved CWS performance, the relationship between the degree to which the network model represents the actual distribution system and its operations and CWS performance has not been quantified. In this paper we examine quantitatively how lack of structural detail in the network model affects CWS performance. We do not consider potential effects of inaccuracies in the representation of distribution system operations.
Studies have examined the influence of uncertainty in various factors on the design of CWSs. Most studied has been the influence of uncertainty in the nature of potential contamination events; Davis et al. (2013) provide a recent review of work in this area. Studies also have considered the influence of uncertainty in water demand (Berry et al., 2006; Comboul and Ghanem, 2012; Cozzolino et al., 2006, 2011; Mukherjee et al., 2017; Ostfeld and Salomons, 2005a, b; Shastri and Diwekar, 2006) and population density (Davis et al., 2013; Rico-Ramirez et al., 2007). Davis et al. (2013) also considered the influence of uncertainty in the rate of contaminant decay in a network following injection and uncertainty in the nature of the exposure model used to assess the consequences of a contamination event. We are not aware of any studies that have examined the influence on CWS design of uncertainties in the nature of the network itself, specifically the accuracy with which the network model used as the basis for designing a CWS represents the actual structure, the pipes and junctions, of the distribution system being considered.
In addition to the influence of uncertainty in the various factors just discussed on the performance of a CWS, the design objective used for the system can also affect its performance when faced with uncertainties. When the nature of potential contamination events is uncertain and the objective is to minimize worst-case adverse consequences associated with the events, CWSs designed to minimize mean-case consequences are more robust than those designed to minimize worst-case consequences (Davis et al., 2013). These designs are called mean-case and worst-case designs, respectively. Mean-case designs are more effective at reducing consequences over a range of conditions. The relative lack of robustness of worst-case designs is a consequence of the narrow focus of these designs, which handicaps their performance when conditions differ from those assumed as the basis for the design.
The primary goal of this paper is to examine how and to quantify to what extent limitations in the detail available on a system's pipes and junctions affect the performance of a CWS design. An additional goal of this paper is to obtain some insight into the robustness of worst- and mean-case designs for a CWS when there are such limitations in the network model used to represent a WDS.
Contamination in a distribution system has the potential to cause a variety of adverse effects. This paper considers adverse health effects associated with the ingestion of contaminated tap water; quantities of ingested contaminant, ingestion doses, are determined for those individuals who are potentially exposed to contaminated water. The term dose level is used to indicate the quantity of ingested contaminant for which adverse consequences are quantified. For a particular contaminant, dose level can be related to a health-effect level. For example, a dose level could correspond to the median lethal dose or the no-observed-adverse-effect level. Lower dose levels can be related to a particular health-effect level for more toxic chemical contaminants and higher dose levels can be related to the same health-effect level for less toxic contaminants. In this paper when high or low dose levels are discussed, a statement is sometimes added that these can be related to contaminants with relatively low or high toxicity, respectively, to re-emphasize this point. The measure of adverse consequences associated with a contamination event that is used in this paper, called impact, is the number of people who receive a dose of a contaminant above some dose level due to the ingestion of contaminated tap water. In this paper the performance of a CWS is defined by the impact that occurs before the CWS detects the presence of contamination.
The analysis presented in this paper is based on case studies using two WDSs. The best available network models for the two systems were used to represent the actual distribution systems, and skeletonized versions of these network models were used as proxies for incomplete network models that might be developed for these systems. Network models will always be incomplete to some, generally unknown, degree; using skeletonized network models together with the best available network models allows the potential significance of uncertainties in network models to be studied. CWSs designed to minimize the adverse consequences of ingesting contaminated tap water were developed using the skeletonized models. These CWSs then were utilized in (transplanted into) the complete network models, where their performance was evaluated and compared to the performance of designs developed using the complete network models. This approach allows the influence of uncertainties in network model detail on CWS performance to be evaluated. Developing and transplanting both worst- and mean-case designs allows the relative robustness of these designs to be studied.
Implementing the approach described above for actual distribution systems requires the following: the availability of reasonably complete (“all-pipes”) models for the WDSs, an approach to skeletonizing these models, a method for designing CWSs, and a method for evaluating the performance of the designs. Except for the evaluation of the performance of transplanted CWS designs developed using skeletonized network models, the methods used here have been documented in previous publications. The approach used here will be outlined with references provided to previous work.
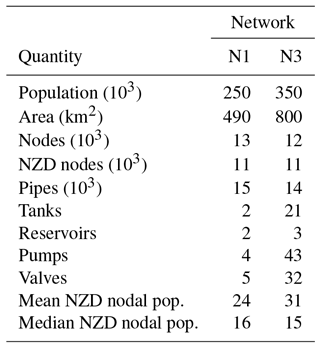
Designs for CWSs were developed using the original and skeletonized versions of the network models for two WDSs. The characteristics of the utility-developed network models used are summarized in Table 1, which provides the populations and areas served, numbers of nodes and pipes in the network models, the number of tanks, reservoirs, pumps, and valves in the models, as well as mean and median nodal populations. Network N1 is a looped system; N3 is a branched system. The WDS represented by Network N1 is located in a relatively flat area, with only a few pressure zones. N3 represents a WDS located in a substantially more complicated environment and has about 10 pressure zones.
The network models were skeletonized using commercially available software to produce models with three levels of skeletonization (20, 30, and 40 cm trims). All pipes having the specified or smaller diameter were trimmed or merged. The methodology used for skeletonization is discussed in Appendix A and is the same as we have used previously (Davis and Janke, 2014). Our results should be reproducible if the same, consistent process described here is applied. Skeletonization software generally uses the methods presented in Walski et al. (2003); Berry et al. (2012) have shown that different skeletonization software generally provides similar results. Table 2 summarizes the characteristics of the skeletonized network models. Note that the ratio of the number of pipes to the number of nodes increases as the level of skeletonization increases, illustrating the effect of the skeletonization process. The networks examined here (N1 and N3) are two of the three networks used in Davis and Janke (2014). Network N1 is also Network 2 in Ostfeld et al. (2008).
Table 1Network descriptions. All numbers in this table are rounded independently to two significant figures. NZD: nonzero demand.
Network skeletonization affects the flow of water through the network, which in turn affects contaminant transport. The discussion here focuses on the implications of this change in contaminant transport for the design of warning systems. A discussion of the hydraulic effects of the skeletonization of the two networks considered here is provided in Appendix B.
Table 2Network skeletonization. All numbers in this table are rounded independently to two significant figures. NZDN: nonzero demand node.

Developing the design for a CWS requires the definition of a design-basis threat and the quantification of the potential adverse effects associated with that threat. A CWS is designed to provide protection against these adverse effects. The threat considered here is the potential injection of a fixed quantity of contaminant at any one of the nodes in a network or at any of the nonzero demand (NZD) nodes in the network. The adverse effects examined are the impacts (as defined above) associated with an injection at a network node. Contaminant injection, transport, and ingestion were simulated using TEVA-SPOT (US EPA, 2017). TEVA-SPOT uses Version 2.00.12 of EPANET (Rossman, 2000) for calculations involving contaminant transport. The analysis here assumes 0.5 kg injections of a conservative contaminant over a 1 h period beginning at 00:00 local time. All simulations were 168 h in duration, which includes the 1 h injection. The simulations used a 1 s water-quality time step and a 1 h hydraulic time step. One second is the shortest water-quality time step that can be used with EPANET.
Contaminant mass imbalances can occur during water-quality simulations with EPANET (Davis et al., 2018). Large imbalances can be associated with elevated estimates for impacts. However, mass imbalances generally can be minimized using short water-quality time steps. The 1 s water-quality time step used here minimizes the potential for any mass imbalances during the water-quality simulations used in this study.
Determining impacts, which the CWSs considered in this paper were designed to minimize, requires nodal populations and the quantity of contaminant ingested by each of the individuals in those populations during a contamination event to be estimated. Nodal population is not provided in the network models; it was assumed to be proportional to nodal water demand. We also assumed that all persons served by a WDS could potentially be exposed to contaminated water. Contaminant concentrations in a network vary both temporally and spatially following injection of a contaminant. Estimating ingestion doses, which are required to determine impacts, therefore requires the times when each individual in the network will be ingesting tap water to be estimated. The quantity of water ingested for each ingestion event also needs to be estimated. Ingestion times were obtained with a probabilistic model developed based on time-use studies (Davis and Janke, 2008, 2009), which assumes that there are five daily ingestion events for each individual. A probabilistic model was also used for daily ingestion volume. An empirical distribution for daily water volume was developed using estimated per capita water volumes ingested by consumers of community water in the United States (US EPA, 2000, 2004). Random values for daily water volumes for each individual at each node in a network were then obtained from this distribution by inverse transform sampling. These daily volumes were then divided equally among an individual's five daily ingestion events. Individuals were assumed to ingest the same volume of tap water each day during the simulation. The methodology used in carrying out these simulations is the same as that discussed in Davis et al. (2014) and is incorporated in TEVA-SPOT.
Using TEVA-SPOT, CWSs were designed to minimize worst- and mean-case impacts associated with the design-basis threat subject to a constraint on the number of sensors. Development of CWS designs is discussed in Davis et al. (2013). TEVA-SPOT optimizes sensor placement using a heuristic approach (Berry et al., 2006). Designs were developed for the original and the three skeletonized network models for each WDS for three sensor set sizes (5, 10, and 25 sensors) and for five different dose levels ranging from 10−4 to 1 mg. A total of 120 designs were developed for each network (two objectives, four network models, three sensor set sizes, and five dose levels).
Sensors in CWSs were assumed to perform perfectly: they detect all contaminants and make no errors. A zero response time was assumed; all water use stops immediately when a contaminant is detected. This paper does not consider the sensitivity of consequences to sensor behavior and response time. These assumptions simplify the analysis. Imperfections in sensor behavior and delays in response will increase consequences relative to those reported here. CWS sensors are arrayed at locations within a network according to designs developed as described above and in the following paragraphs. CWSs alert when any sensor detects contamination during an event. Impact is determined by summing the number of receptors at all nodes who have received doses above some dose level when the system alerts. The worst-case and mean-case performances of a CWS are determined by the largest impact and the mean impact, respectively, associated with a threat before contamination is detected by a sensor.
The performance of the CWS designs developed for the original and skeletonized network models for each WDS was evaluated using the original network model for the system. Worst-case impacts were determined using both worst-case and mean-case designs. To evaluate the performance of a design developed using a skeletonized network model but applied to the original network model, the locations of the sensors determined for the skeletonized network were used to define a sensor network for the original model, and impacts were determined using this transplanted CWS. TEVA-SPOT has a built-in capability, the Regret Analysis mode, that allows various designs to be easily evaluated and that facilitates the selection of the best sensor design among those being considered (US EPA, 2017).
The approach described yields impacts for CWSs designed using the original network models as well as impacts for CWS designs developed using the skeletonized network models that have been transplanted into the original models. Impacts determined using the transplanted designs were compared with those determined using the original designs to obtain insights into the extent to which CWS performance is adversely affected when designs are developed using incomplete information on a WDS. Comparing the relative worst-case performances of the transplanted worst- and mean-case designs provides insight into the robustness of these designs when there is uncertainty in the network model.
The heuristic method used for sensor placement generally produces optimal designs, but in some cases can produce designs that are suboptimal (Davis et al., 2013). For the original model for Network N1 there were two instances of obvious suboptimality for worst-case designs out of the 15 cases (three sensor set sizes and five dose levels) examined; for Network N3 there was one. A design is suboptimal if larger impacts are obtained when the conditions used in the design and its evaluation are the same than when such conditions differ. Results were corrected to help minimize the effect of such obvious suboptimalities for a particular sensor set size and dose level by using the smallest impact from the five designs developed for different dose levels for that number of sensors. The corrections resulted in reductions in impacts of 6 and 18 % for the two instances of suboptimality for Network N1 and a 9 % reduction for the single instance for Network N3. The correction does not identify the optimal design; it only helps improve the estimate of impacts that would be obtained with the optimal design.
This section considers two topics: (1) CWS performance given uncertainty in the structural details of the network model and (2) the robustness of mean- and worst-case CWS designs when there is such uncertainty in the network model. CWS performance is discussed in terms of the performance of the overall system and in terms of the performance of the individual sensors in a system.
3.1 CWS performance: overall system
CWSs developed using the skeletonized network models generally perform more poorly than do those developed using the original network model. The following paragraphs discuss the behavior of these different CWSs.
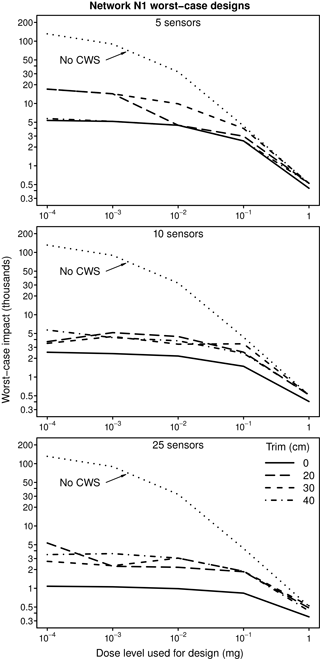
The plots in Fig. 1 compare estimated impacts for worst-case CWS designs developed for three sensor set sizes using the original and skeletonized network models for Network N1. In this figure, the designs developed using the skeletonized network models are non-transplanted designs: they are evaluated using the network models for which they were designed. Note the logarithmic scales on both the vertical and horizontal axes. Results are given for four different CWS designs as a function of the dose level used for the design. The CWSs were evaluated using the same dose level as used for their design. Impacts increase as dose level decreases, but are relatively constant at smaller dose levels. Impacts decrease as the number of sensors used in the CWS design increases. The four CWS designs being evaluated for each sensor set size are the design developed using the original network model and the three non-transplanted designs developed using the skeletonized networks. In the figure, a trim of 0 cm corresponds to the original model and the 20, 30, and 40 cm trims correspond to the three levels of skeletonization used. The estimated impacts obtained using the skeletonized network models are similar to those obtained using the original network model. However, if CWSs are designed using a skeletonized (i.e., an incomplete) network model and then implemented, they will be used in actual system, which is better approximated by the original network model. The performance of transplanted designs is discussed next.
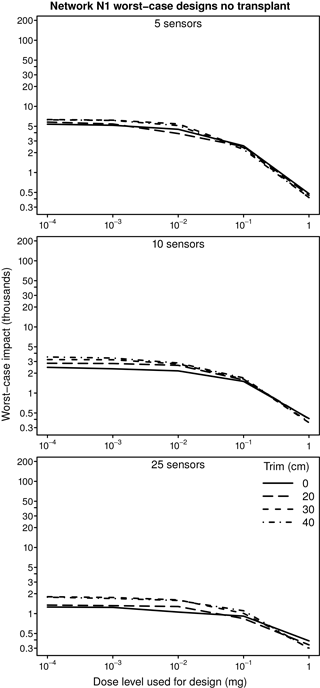
Figure 1Worst-case impact versus dose level for original and non-transplanted, worst-case CWS designs for Network N1. Results are shown for the original model and three levels of network skeletonization (trims).
Again using Network N1, the plots in Fig. 2 compare (1) estimated impacts obtained when the CWS designs developed using the skeletonized models are transplanted into the original network model with (2) impacts estimated for the CWS designed using the original network model. The plots also show estimated worst-case impacts when no CWS is used. Note the logarithmic scales on the vertical and horizontal axes. The differences between the impacts estimated for the designs developed for the original and the skeletonized network models for Network N1 generally become larger when the designs for the skeletonized network model are transplanted into the original network model.
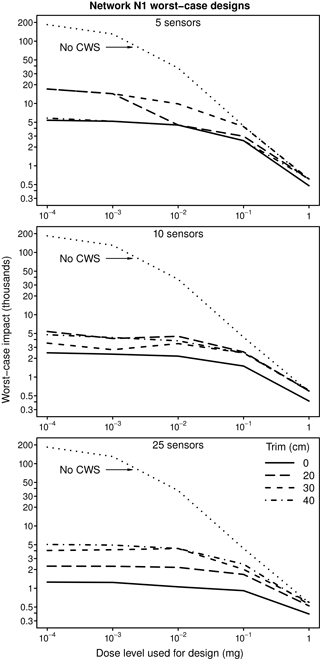
Figure 2Worst-case impact versus dose level for original and transplanted worst-case CWS designs for Network N1. Results are shown for the original model and three levels of network skeletonization (trims).
The analysis presented in this paper used an injection mass of 0.5 kg. If desired, figures that provide results as a function of dose level can be rescaled to show results for different injection masses. The plots in Figs. 1 and 2 and in other figures that present results as a function of dose level would have the same shape if a different injection mass were used. However, if the injected mass is changed by some factor, the values on the horizontal axis also need to be changed by the same factor. For example, if the injection mass is 5 kg instead of 0.5 kg, the values on the horizontal axis in Figs. 1 and 2 need to be multiplied by 10. Use of a different injection mass in our analysis would not affect the conclusions presented in this paper.
The plots in Fig. 3 provide a comparison for Network N1 of the impacts obtained using designs developed for the skeletonized network models when they are used in the skeletonized network models (non-transplanted designs) and when they are transplanted into the original network model. The same design is being used, but evaluated using different network models. Depending on the dose level and number of sensors, the impacts estimated for Network N1 can be 2 to 3 times larger when the designs are used in the original network rather than in the skeletonized network where they were developed. In other words, evaluating a CWS using the skeletonized network model for which it was designed can yield results that considerably underestimate the actual consequences that could occur if the design were used in the actual WDS. There is no consistent pattern in impacts or relative impacts related to the level of skeletonization used. Note that the somewhat jagged nature of some of the lines in the plots in Fig. 3 is the result of using only five points to construct the lines in the plots in this (and other similar) figures.

Figure 3Relative worst-case impacts for transplanted and non-transplanted worst-case CWS designs for Network N1. Results are shown for three levels of network skeletonization (trims).
The estimated percentage reductions in impacts obtained using the CWSs designed for Network N1 relative to the worst-case impacts estimated for the network when no CWS is used are shown in the plots in Fig. 4. (When no CWS is used, the relative reduction in impacts is 0 %.) The reduction in impacts for low dose levels (contaminants with relatively high toxicity) can be similar and substantial (generally near or > 90 % for dose levels below about 0.01 mg) for the original and transplanted designs. However, at higher dose levels (contaminants with relatively low toxicity), the reduction in impacts obtained with transplanted designs can be considerably smaller than that obtained with the original design. The reduction in impacts does not show a consistent relationship with the level of skeletonization. Percentage reduction in impacts decreases as dose level increases. Consequences associated with less toxic contaminants generally are more localized than those associated with more toxic contaminants because of the larger quantity of contaminant required to produce a similar health effect. CWSs are less effective in providing protection against localized effects than effects that are more widespread.

Figure 4Reduction in worst-case impacts obtained with original and transplanted worst-case CWS designs for Network N1 relative to impacts obtained when no CWS is used. Results are shown for the original model and three levels of network skeletonization (trims).
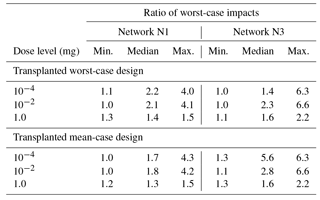
Table 3Ratios of worst-case impacts obtained with transplanted and original CWS designs. Ratio refers to the ratio of the worst-case impact obtained with the transplanted design divided by the worst-case impact obtained with the worst-case design developed using the original network model. Minimum (Min.), median, and maximum (Max.) values for the ratio are given for the nine ratios determined for the three sensor set sizes and the three skeletonizations.
Impacts estimated for CWSs designed using Network N3 are shown in the plots in Fig. 5, which provides results similar to those in Fig. 2 for Network N1. The results for Network N3 are more consistent than those for Network N1, with impacts generally increasing with increasing level of skeletonization. The plots in Fig. 6 give the ratio of impacts for transplanted and non-transplanted designs for Network N3. The ratios are generally larger than those for Network N1 (Fig. 3) when 10 or 25 sensors are used. (Note the difference between the vertical scales used in Figs. 3 and 6.) When designed and evaluated using the skeletonized network models for Network N3, the results for designs with 10 or 25 sensors underestimate by a factor of 2 to 8 times the impacts expected if the design were used in the actual network, a larger underestimate than for Network N1. For five sensors, the underestimate can be as much as a factor of 2. As is the case for Network N1, the percentage reductions in impacts at larger dose levels achieved using the transplanted CWS designs are generally considerably less than those obtained using designs developed using the original network model, as shown in Fig. 7.
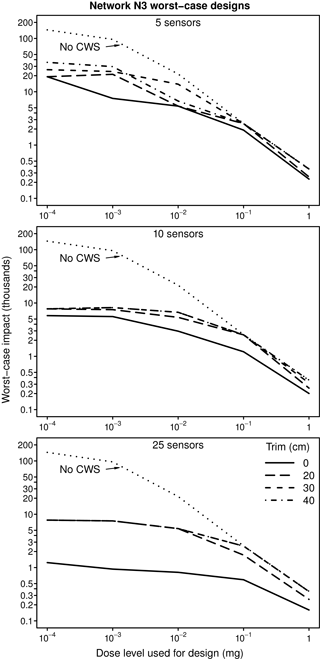
Figure 5Worst-case impact versus dose level for original and transplanted, worst-case CWS designs for Network N3. Results are shown for the original model and three levels of network skeletonization (trims).
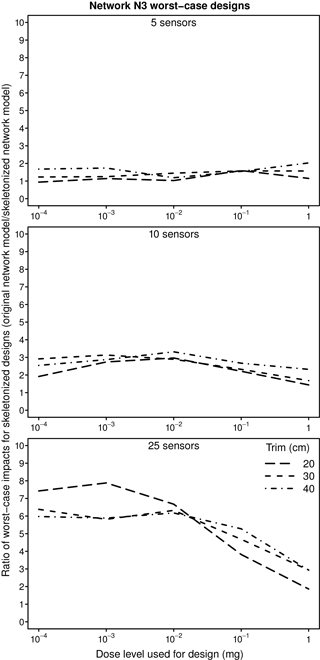
Figure 6Relative worst-case impacts for transplanted and non-transplanted worst-case CWS designs for Network N3. Results are shown for three levels of network skeletonization (trims).
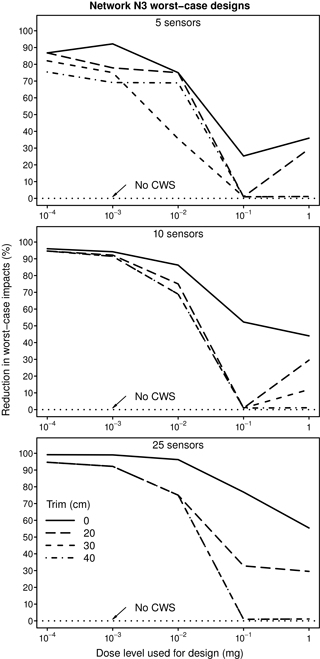
Figure 7Reduction in worst-case impacts obtained with original and transplanted worst-case CWS designs for Network N3 relative to impacts obtained when no CWS is used. Results are shown for the original model and three levels of network skeletonization (trims).
The relative performance of the transplanted worst- and mean-case CWS designs for Networks N1 and N3 is summarized in Table 3. Performance is relative to the performance of a CWS designed to minimize worst-case impacts using the original network model. For several dose levels, the table gives the range (maximum and minimum values) in the ratios of worst-case impacts obtained with the transplanted design to the worst-case impacts obtained with the original worst-case design, as well as the median value of the ratio. The results shown for each network and dose level are based on the nine ratios determined using three sensor set sizes and three levels of skeletonization. For example, for the 1.0 mg dose level for Network N1 and the transplanted worst-case design, the minimum value of the ratio of worst-case impacts obtained with the transplanted worst-case design to the impact obtained with the original worst case design is 1.3. The largest value of the ratio is 1.5 and the median for the nine ratios is 1.4.
The results in Table 3 indicate that for Networks N1 and N3 the relative performance of the transplanted worst-case designs generally becomes poorer when the dose level is smaller than 1.0 mg. In particular, the median and maximum values of the ratios for the two networks generally increase when the dose level decreases below 1.0 mg. The maximum ratios are generally considerably larger for Network N3 than for Network N1, indicating that the relative performance of the transplanted designs is network-dependent. Note that although the relative performance of the transplanted designs is poorer at smaller dose levels, the reduction in impacts, both percentagewise and in absolute terms, is considerably better at smaller dose levels than at 1.0 mg.
The results in Table 3 also show that the relative performance of the transplanted mean-case designs deteriorates when the dose level decreases below 1.0 mg. The results in the table show that the relative worst-case performance of the transplanted mean-case designs is generally similar to the relative worst-case performance of the transplanted worst-case designs: the ratios for the transplanted mean-case designs are generally similar to the corresponding ratios for the transplanted worst-case designs.
CWS performance is influenced by the network nodes considered as possible injection locations. Figure 8 provides results for Network N1 similar to those shown in Fig. 2 except that only NZD nodes are used as injection locations. Differences in the performances of the transplanted designs obtained with all nodes (Fig. 2) or only NZD nodes (Fig. 8) are noticeable when 10 or 25 sensors are used. Worst-case impacts with no CWS are somewhat smaller when only NZD nodes are used relative to those obtained when all nodes are considered as possible injection locations.
3.2 CWS performance: individual sensors
The preceding discussion has examined the performance of CWSs as systems. Examining the performance of individual sensors in those systems provides some additional insight into how the overall systems perform. CWS designs were developed considering their performance when challenged by the possible injection of contaminants at any node in the network or at any NZD node. A CWS can detect some of the events, but, in general, with a limited number of sensors will not detect all events. The worst-case performance of a CWS is determined by the largest impact associated with any event that occurs before an event is detected by a sensor. For Network N1 with a five-sensor CWS and injections at NZD nodes, the sensors detect about 3500 events out of about 11 000, for a dose level of 10−4 mg. The number of events detected for the original network model does decrease somewhat as the level of skeletonization increases, from about 3600 for the original design to about 3500 for the 20 cm transplanted design and to about 3450 for the 40 cm transplanted design. About 7000 events have not been detected by any sensor when the CWS designs first detect an event. The maximum impacts for undetected events are about 5000, 4800, and 5700 for the original, 20 cm, and 40 cm designs, respectively. The optimization process should minimize worst-case impacts but does not attempt to minimize other impacts, either detected or not. For the case considered here, the largest impacts for undetected events are smaller than the worst-case impacts. Therefore, it is not unexpected that the largest undetected impact for the original design (5000) is somewhat larger than the largest undetected impact for the 20 cm transplanted design (4800).
The performance of the individual sensors in the five-sensor CWS design developed using the original network and the five-sensor, 20 and 40 cm transplanted designs is shown in Fig. 9 for a dose level of 10−4 mg. Note that the vertical scale on the plot for the 20 cm design is different from the vertical scale used in the other two plots. The figure shows results considering NZD nodes as injection locations. The general locations of the five widely spaced sensors in the three designs are similar and the sensors are arbitrarily labeled as Sensors 1 through 5, consistently for all the designs. For the detected events, the impacts at the time the events are detected were sorted in ascending order for each of the five sensors and plotted against event number, starting with the lowest impact event for Sensor 1 and continuing using a cumulative count of events through the highest impact event for Sensor 5. The numbering of events in the three plots in Fig. 9 is independent. The highest impact for any event detected by any sensor is the worst-case impact for the CWS unless a higher impact is associated with any of the undetected events. No undetected events with such higher impacts occur for Network N1 and five sensors, as noted above.

Figure 9Performance of individual sensors for five-sensor, worst-case CWS designs for Network N1 and a dose level of 10−4 mg obtained using nonzero demand nodes as possible injection locations. Sensor numbers (1 through 5) are shown in the upper plot. Results are presented for CWSs developed using the original network model and two skeletonized models. Evaluations of CWS performance used the original network model.
In Fig. 9, the results for each of the five sensors are presented from left to right, with the results labeled with the sensor number in the upper plot. As an example of how to interpret the plots in the figure, in the upper plot the results for Sensor 4 begin at about Event 800 and continue to about Event 2200; about 1400 events are detected by this sensor. The maximum impact for any impact detected by the sensor is about 2500. The highest impact for any event detected by any sensor is over 5000 for Sensor 5. This is the worst-case impact for the CWS.
The performance of the sensors varies substantially between the original and transplanted designs. The worst-case impact for the original design is over 5000, as already noted, over 16 000 for the transplanted 20 cm design, and over 5000 for the transplanted 40 cm design, similar to that for the original design, but for a different sensor. The three worst-case impacts in Fig. 9 correspond to the worst-case impacts in the upper plot in Fig. 8 for a dose level of 10−4 mg. Figure 8 shows that the worst-case impacts for the original and 40 cm designs for five sensors are similar at that dose level. Figure 9 shows that these impacts were the result of events observed by different sensors. Although not shown in the figure, the events in the two cases are also different. Figure 8 suggests that the original and 40 cm, five-sensor designs perform similarly for a dose level of 10−4 mg. In fact, the similarity results from sensors in different parts of the network detecting different events with the same impacts.
3.3 Robustness of mean- and worst-case designs
Figures 10 and 11 provide a direct comparison of the worst-case impacts obtained with the transplanted mean- and worst-case designs for Networks N1 and N3. The figures are scatterplots of the impacts obtained with the two types of transplanted designs. Note the logarithmic scales on the vertical and horizontal axes. For each network, results are given for three sensors set sizes, three levels of skeletonization, and five dose levels, for a total of 45 comparisons in each figure. Some points in the figures overlap or are clustered closely together. For points that lie above the diagonal lines in the figures, the transplanted mean-case design yields smaller worst-case impacts than the transplanted worst-case design. For points below the lines, the worst-case design yields smaller impacts. For points on the line, both designs provide the same impacts.
For Network N1 there are 27 points in Fig. 10 that lie above the diagonal line, 9 points that lie on the line, and 9 points that lie below the line. For the comparisons used in Fig. 10, the transplanted mean-case designs yield worst-case impacts that are less than or equal to those yielded by the transplanted worst-case designs in 36 of the 45 cases for Network N1. The transplanted worst-case designs yield worst-case impacts that are less than or equal to those obtained for the transplanted mean-case designs in 18 of the 45 cases. For the 27 instances in which impacts for the worst-case designs exceed those for the mean-case designs, the impacts are about 34 % larger on average. For the 9 instances in which the impacts for the mean-case designs are larger, they are about 59 % larger on average. Considering only NZD nodes (not plotted), the transplanted mean-case designs perform as well as or better than the transplanted worst-case designs in 32 of the 45 cases; transplanted worst-case designs perform as well as or better than transplanted mean-case designs in 28 of the 45 cases.
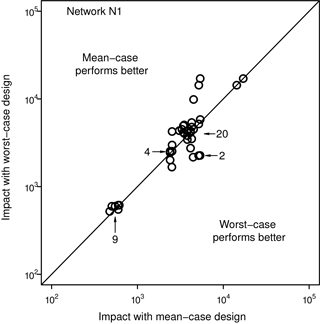
Figure 10Comparison of worst-case impacts for transplanted mean- and worst-case CWS designs for Network N1 (numbers and arrows indicate overlapping or clustered points).
For Network N3 there are 6 points in Fig. 11 that lie above the diagonal, 27 points that lie on the line, and 12 points that lie below the line. The transplanted mean-case designs yield impacts less than or equal to those for the worst-case designs in 33 of the 45 cases for Network N3. The transplanted worst-case designs yield worst-case impacts that are less than or equal to those obtained with the transplanted mean-case designs in 39 of the 45 cases. For the 6 instances in which impacts for the worst-case designs exceed those for the mean-case designs, the impacts are about 96 % larger on average. For the 12 instances in which the impacts for the mean-case designs are larger, they are about 120 % larger on average. Considering only NZD nodes (not plotted), the transplanted mean-case designs perform as well as or better than the transplanted worst-case designs in 28 of the 45 cases; transplanted worst-case designs perform as well as or better than transplanted mean-case designs in 38 of the 45 cases.
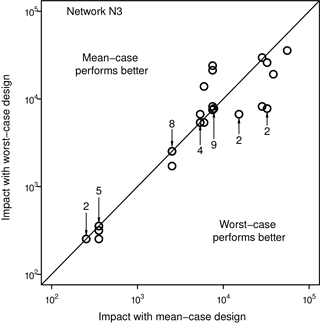
Figure 11Comparison of worst-case impacts for transplanted mean- and worst-case CWS designs for Network N3 (numbers and arrows indicate overlapping or clustered points).
For the two networks studied, the mean-case designs developed using the skeletonized network models yield results that are comparable to those obtained with the worst-case designs developed using the skeletonized network models when the designs are transplanted into the original network models. Mean-case designs perform somewhat better for Network N1 and somewhat poorer for Network N3. As discussed above, mean-case designs are more robust than worst-case designs when the objective is to minimize worst-case impacts and there is uncertainty concerning the conditions of a contamination event. The results presented here for Networks N1 and N3 indicate that transplanted mean-case and worst-case designs can be similarly robust when used to estimate worst-case impacts in the original network models. The small sample size limits the ability to make any more general conclusions about the overall robustness of mean-case designs under conditions of uncertainty in the network model. Evaluations using additional networks would be helpful.
On the basis of the two networks examined, lack of structural detail in the network model results in worst-case CWS designs that perform more poorly than worst-case designs developed using the original all-pipes network model. The relative performance of the designs developed using incomplete network models, as measured by the reduction in worst-case impacts, generally improves as the dose level decreases. Nevertheless, at smaller dose levels (more toxic contaminants) a lack of network model detail can yield CWS designs that have worst-case impacts several times larger than those obtained using a much more complete network model.
Designing and evaluating a CWS using an incomplete network model can result in a substantial underestimate of the consequences that could occur if the design were used in the actual WDS. The difference depends on the network, dose level, and number of sensors; however, for the cases considered in this paper, estimated impacts can increase by a factor of 2 to 8 times when the design is evaluated using the complete network model.
Although lack of model detail generally has an adverse effect on CWS performance, no simple relationship was found between the degree of skeletonization and loss of performance. For the two networks studied, the relationship depends on the number of sensors used in the CWS.
In spite of the negative effect of loss of network model structural detail on CWS performance, CWSs designed using incomplete network models can provide substantial reductions in adverse consequences compared to results obtained when no CWS is used, except at high dose levels (less toxic contaminants), for which consequences tend to be localized near the injection location. Reductions at low dose levels are generally above 70 % for the skeletonized networks and consequences considered.
Proper understanding of the basis for CWS performance requires an understanding of the performance of the individual sensors used in the CWS. As discussed for Network N1, apparently similar overall performance of two different CWS designs can be associated with very different results for the individual sensors in the system.
Mean-case designs developed using incomplete network models can provide worst-case results that are generally comparable to those obtained with worst-case designs developed using the same incomplete models, consistent with a conclusion that mean-case designs can provide robust results under conditions of uncertainty. However, results for more networks are needed before any broader conclusions can be made.
Improvements in network models, by reducing the uncertainty in their structural details, have the potential to yield significantly better performing CWSs. The magnitude of the potential improvement depends on the degree of the improvement in the network model and the nature of the contaminants of most concern. However, the results for the networks examined here suggest that a reduction in worst-case impacts by a factor of as much as about 2 or more is possible for contaminants whose effects are not localized near the injection location (cf. Table 3). In addition, evaluations of the expected performance of CWSs designed using all-pipes models should provide considerably more realistic results than evaluations of designs developed with incomplete network models, which yielded substantial (2 to 8 times) underestimates of impacts for the two networks examined.
The results presented here should be useful to those responsible for designing or implementing CWSs, in particular managers and engineers in water utilities. Hopefully, the results will help provide motivation for the improvement of existing network models.
The original and skeletonized network models (.inp files) for Network N1 are available in the Supplement. The model for Network N3 is proprietary and cannot be shared.
We skeletonized Networks N1 and N3 using a commercial software package, InfoWater® Skeletonizer (Innovyze, 2005). This package allows three methods to be used for skeletonization, namely branch trimming, parallel pipe merging, and series pipe merging. It maintains total network demand by recalculating and reallocating demands at all affected nodes. Pipes with check valves or controls are not included in the skeletonization process. Because the order in which trimming and merging are performed can affect the configuration of the skeletonized network (Innovyze, 2005), we followed a consistent process when skeletonizing networks.
We began the skeletonization process by specifying the pipe diameters to be considered (namely ≤ 20, 30, and 40 cm) using a query in the software's domain manager. Networks were then skeletonized; dead-end pipes were trimmed, series pipes were reduced, and equivalent pipes were obtained by merging parallel pipes and then series pipes. (The software has specific options for (1) dead-end trimming, (2) series pipe reduction, and (3) maintaining hydraulic equivalency.)
When we performed dead-end trimming, we did not use any secondary options. Therefore, maximum trimming reductions were carried out for each iteration of the trimming process. When series pipe reduction was carried out, we specified that the pipe ID/attribute retain choice be large diameter and that the demand distribution method be nearest junction. No additional options were used for series pipe reduction. Secondary options were specified for hydraulic equivalency: larger diameter was selected for the pipe ID/attribute retain choice as was the equivalent diameter check box. We performed parallel and series merges using the merge parallel and merge series options. The number of junctions was not affected by the former; there was some decrease in the number of pipes. The series merge reduced the number of both pipes and nodes.
We consistently and iteratively carried out trimming, reducing, and merging, both parallel and series, on each network. We first performed trimming, then reducing, and finally merging for each of the three trim levels used. Five iterations were carried out to achieve maximum reduction in the number of pipes and nodes. Parallel merging was always done before series merging and was executed immediately after using the reduction option.
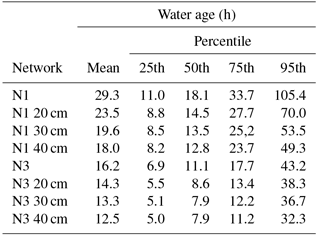
Skeletonization affects estimated flow velocities and, consequently, water ages. Table B1 provides mean and median flow velocities for the original and skeletonized versions of Networks N1 and N3. Mean and median velocities increase substantially with the first level (20 cm) of skeletonization and then plateau or decrease slightly with additional skeletonization, consistent with the results reported by Bahadur et al. (2008).
The skeletonization process removes pipes with diameters below a certain size. The process largely influences flow velocities in pipes with diameters that are affected by the trimming process. Tables B2 and B3 provide statistics on flow velocities for pipes in Networks N1 and N3, with diameters that are affected and unaffected by the trimming process. The tables show results for both the original network models and for the skeletonized models with 20 and 40 cm trims. Mean flow velocities and velocities ranging from the 25th to the 95th percentiles in pipes with diameters less that or equal to the trim level are substantially increased by skeletonization for the two trim levels shown for both Networks N1 and N3. However, there is little change in the statistics for flow velocities for pipes with diameters greater than the trim level. For example, compare velocities in Table B2 for Networks N1 and N1 20 cm for pipes with diameters less than or equal to 20 cm. The skeletonized network has a considerably higher mean velocity (0.10 versus 0.06 m s−1), as well as considerably higher velocities for the four percentiles shown. In the same table, compare velocities for Networks N1 and N1 40 cm for pipes with diameters greater than 40 cm. The mean velocities (0.33 and 0.32 m s−1), as well as velocities for the four percentiles shown, are similar for the original and skeletonized models. Note in Tables B2 and B3 that the fraction of pipes with diameters at or below the trim level is generally substantially larger than the portion with diameters above the trim level, even after skeletonization, especially for the 40 cm trim. For example, from Table B3, the fraction of pipes in Network N3 with diameters greater than 40 cm is only 0.04 and for N3 40 cm it is only 0.13.
Table B1Mean and median flow velocities, Networks N1 and N3, determined for the last 24 h of a 168 h simulation, using a 1 h hydraulic time step.
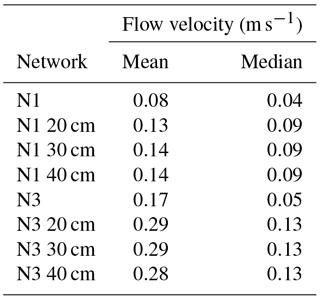
Table B2Network N1 flow velocities, determined for the last 24 h of a 168 h simulation, using a 1 h hydraulic time step.
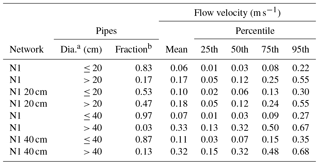
a Pipe diameters considered. b Fraction of network pipes included.
Table B3Network N3 flow velocities, determined for the last 24 h of a 168 h simulation, using a 1 h hydraulic time step.
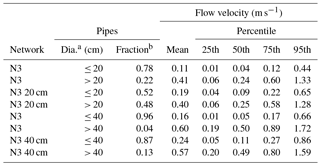
a Pipe diameters considered. b Fraction of network pipes included.
Table B4 provides statistics on water ages for the original and trimmed models for Networks N1 and N3. Mean water age for the original and skeletonized models for Network N1 decreases with the level of skeletonization, as do the 25th, 50th, 75th, and 95th percentile water ages. Results are similar for Network N3, except for the median water age for the 30 and 40 cm trims, which has stabilized at 7.9 h. The effect of skeletonization on mean water age for the two networks is consistent with the findings of Bahadur et al. (2008).
The supplement related to this article is available online at: https://doi.org/10.5194/dwes-11-49-2018-supplement.
The authors declare that they have no conflict of interest.
This paper has been subjected to the US Environmental Protection Agency's (EPA's) review and has been approved for publication. The views expressed in this paper are those of the authors and approval does not signify that the contents necessarily reflect the views of the Agency. Mention of trade names, products, or services does not convey official EPA approval, endorsement, or recommendation. Because of the confidentiality of the information, the identity of the real WDSs used in this paper and any information that could be used to identify the systems cannot be disclosed.
EPA's Office of Research and Development funded, managed, and participated in
the research described here under an interagency agreement. Work at Argonne
National Laboratory was sponsored by the EPA under an interagency agreement
through US Department of Energy Contract DE-AC02-06CH11357. We appreciate the
helpful comments provided by three anonymous referees.
Edited by: Atul Mittal
Reviewed by: three anonymous referees
Bahadur, R., Johnson, J., Janke, R., and Samuels, W. B.: Impact of model skeletonization on water distribution model parameters as related to water quality and contaminant consequence assessment, Water Distribution System Analysis Symp. 2006, 27–30 August 2006, Cincinnati, OH, USA, ASCE, Reston, VA, USA, https://doi.org/10.1061/40941(247)64, 2008. a, b, c
Berry, J., Hart, W. E., Phillips, C. A., Uber, J. G., and Watson, J.-P.: Sensor placement in municipal water networks with temporal integer programming models, J. Water Res. Pl.-ASCE, 132, 218–224, https://doi.org/10.1061/(ASCE)0733-9496(2006)132:4(218), 2006. a, b
Berry, J., Boman, E., Riesen, L. A., Hart, W. E., Phillips, C. A., and Watson, J.-P.: User's manual TEVA-SPOT Toolkit 2.5.2, National Homeland Security Research Center, Office of Research and Development, US Environmental Protection Agency, Cincinnati, OH, USA, EPA 600/R-08/041B, 2012. a
Comboul, M. and Ghanem, R.: The value of information in the design of resilient water distribution sensor networks, J. Water Res. Pl.-ASCE, 139, 449–455, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000259, 2012. a
Cozzolino, L., Mucherino, C., Pianese, D., and Pirozzi, F.: Positioning, within water distribution networks, of monitoring stations aiming at an early detection of intentional contamination, Civ. Eng. Environ. Syst., 23, 161–174, https://doi.org/10.1080/10286600600789359, 2006. a
Cozzolino, L., Della Morte, R., Palumbo, A., and Pianese, D.: Stochastic approaches for sensors placement against intentional contaminations in water distribution systems, Civ. Eng. Environ. Syst., 28, 75–98, https://doi.org/10.1080/10286608.2010.482653, 2011. a
Davis, M. J. and Janke, R.: Importance of exposure model in estimating impacts when a water distribution system is contaminated, J. Water Res. Pl.-ASCE, 134, 449–456, https://doi.org/10.1061/(ASCE)0733-9496(2008)134:5(449), 2008. a
Davis, M. J. and Janke, R.: Development of a probabilistic timing model for the ingestion of tap water, J. Water Res. Pl.-ASCE, 135, 397–405, https://doi.org/10.1061/(ASCE)0733-9496(2009)135:5(397), 2009. a
Davis, M. J. and Janke, R.: Influence of network model detail on estimated health effects of drinking water contamination events, J. Water Res. Pl.-ASCE, 141, 9 pp., https://doi.org/10.1061/(ASCE)WR.1943-5452.0000436, 2014. a, b, c
Davis, M. J., Janke, R., and Phillips, C. A.: Robustness of designs for drinking water contamination warning systems under uncertainty, J. Water Res. Pl.-ASCE, 140, 11 pp., https://doi.org/10.1061/(ASCE)WR.1943-5452.0000408, 2013. a, b, c, d, e, f
Davis, M. J., Janke, R., and Magnuson, M. L.: A framework for estimating the adverse health effects of contamination events in water distribution systems and its application, Risk Anal., 34, 498–513, https://doi.org/10.1111/risa.12107, 2014. a
Davis, M. J., Janke, R., and Taxon, T. N.: Mass imbalances in EPANET water-quality simulations, Drink. Water Eng. Sci., 11, 25–47, https://doi.org/10.5194/dwes-11-25-2018, 2018. a
Grayman, W. M. and Rhee, H.: Assessment of skeletonization in network models, Proc. 2000 Joint Conf. Water Resource Engineering and Water Resources Planning and Management, 30 July–2 August 2000, Minneapolis, MN, USA, ASCE, Reston, VA, USA, https://doi.org/10.1061/40517(2000)196, 2000. a
Grayman, W. M., Males, R. M., and Clark, R. M.: The effects of skeletonization on distribution system modeling, Proc. AWWA Conf. on Computers in the Water Industry, 14–17 April 1991, Houston, TX, USA, American Water Works Association, Denver, CO, USA, 661–684, 1991. a
Hart, W. E. and Murray, R.: Review of sensor placement strategies for contamination warning systems in drinking water distribution systems, J. Water Res. Pl.-ASCE, 136, 611–619, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000081, 2010. a
Innovyze: InfoWater Skeletonizer: users guide, Innovyze, Pasadena, CA, USA, 2005. a, b
Janke, R., Murray, R., Uber, J., Bahadur, R., Taxon, T., and Samuels, W.: Using TEVA to assess impact of model skeletonization on contaminant consequence assessment and sensor placement design, Proc. World Environ. and Water Resources Congress 2007, 15–19 May 2007, Tampa, FL, USA, ASCE, Reston, VA, USA, https://doi.org/10.1061/40927(243)527, 2007. a
Janke, R., Haxton, T. B., Grayman, W., Bahadur, R., Murray, R., Samuels, W., and Taxon, T.: Sensor network design and performance in water systems dominated by multi-story buildings, Proc. World Environ. and Water Resources Congress 2009, 17–21 May 2009, Kansas City, MO, USA, ASCE, Reston, VA, USA, https://doi.org/10.1061/41036(342)46, 2009. a
Klise, K. A., Phillips, C. A., and Janke, R. J.: Two-tiered sensor placement for large water distribution network models, J. Infrastruct. Syst., 19, 465–473, https://doi.org/10.1061/(ASCE)IS.1943-555X.0000156, 2013. a
Mukherjee, R., Diwekar, U. M., and Vaseashta, A.: Optimal sensor placement with mitigation strategy for water network systems under uncertainty, Comput. Chem. Eng., 103, 91–102, https://doi.org/10.1016/j.compchemeng.2017.03.014, 2017. a
Ostfeld, A. and Salomons, E.: Optimal early warning monitoring system layout for water networks security: inclusion of sensors sensitivities and response delays, Civ. Eng. Environ. Syst., 22, 151–169, https://doi.org/10.1080/10286600500308144, 2005a. a
Ostfeld, A. and Salomons, E.: Securing water distribution systems using online contamination monitoring, J. Water Res. Pl.-ASCE, 131, 402–405, https://doi.org/10.1061/(ASCE)0733-9496(2005)131:5(402), 2005b. a
Ostfeld, A., Uber, J. G., Salomons, E., Berry, J. W., Hart, W. E., Phillips, C. A., Watson, J-P., Dorini, G., Jonkergouw, P., Kapelan, Z., di Pierro, F., Khu, S-T., Savic, D., Eliades, D., Polycarpou, M., Ghimire, S. R., Barkdoll, B. D., Gueli, R., Huang, J. J., McBean, E. A., James, W., Krause, A., Leskovec, J., Isovitsch, S., Xu, J., Guestrin, C., VanBriesen, J., Small, M., Fischbeck, P., Preis, A., Propato, M., Piller, O., Trachtman, G. B., Wu, Z. Y., and Walski, T.: The battle of the water sensor networks (BWSN): A design challenge for engineers and algorithms, J. Water Res. Pl.-ASCE, 134, 556–568, https://doi.org/10.1061/(ASCE)0733-9496(2008)134:6(556), 2008. a
Rico-Ramirez, V., Frausto-Hernandez, S., Diwekar, U. M., and Hernandez-Castro, S.: Water networks security: A two-stage mixed-integer stochastic program for sensor placement under uncertainty, Comput. Chem. Eng., 31, 565–573, https://doi.org/10.1016/j.compchemeng.2006.08.012, 2007. a
Rossman, L. A.: EPANET 2 users manual, US Environmental Protection Agency (EPA), Office of Research and Development, National Risk Management Research Laboratory, Cincinnati, OH, USA, EPA/600/R-00/057, 2000. a
Shastri, Y. and Diwekar, Y.: Sensor placement in water networks: A stochastic programming approach, J. Water Res. Pl.-ASCE, 132, 192–203, https://doi.org/10.1061/(ASCE)0733-9496(2006)132:3(192), 2006. a
US EPA: Estimated Per Capita Water Ingestion in the United States, Office of Water, Washington, DC, USA, EPA-822-00-008, 2000. a
US EPA: Estimated Per Capita Water Ingestion and Body Weight in the United States – An Update, Office of Water, Washington, DC, USA, EPA-822-R-00-001, 2004. a
US EPA: Models, tools and applications for homeland security research, available at: https://www.epa.gov/homeland-security-research/models-tools-and-applications-homeland-security-research, last access: 3 August 2017. a, b
Walski, T. M., Chase, D. V., Savic, D. A., Grayman, W., Beckwith, S., and Koelle, E.: Advanced water distribution modeling and management, Haestad Press, Waterbury, CT, USA, 2003. a